Es gibt einige Anwendungen, bei denen ein Standard-Einkanalthermometer die Temperatur nicht korrekt misst. Dazu gehören Anwendungen bei denen:
- Das Messobjekt kleiner als der Messfleck ist.
- Die Sicht auf das Messobjekt durch Staub, Rauch oder Dampf beeinträchtigt ist.
- Die Fenster schmutzig bzw. schwer sauber zu halten sind.
- Der Emissionsgrad sich während der Messung ändert.
Quotientenpyrometer (auch Zweifarben- oder Verhältnispyrometer genannt), können die Temperatur auch unter solchen problematischen Bedingungen korrekt messen.
Was ist der Unterschied zwischen einem Zweifarben- und einem Einfarbenpyrometer? Bei einem Zweifarbenpyrometer werden zwei Detektoren verwendet, die beide auf verschiedenen - aber dicht zusammenliegenden - Wellenlängen arbeiten, und auf dasselbe Ziel ausgerichtet sind.
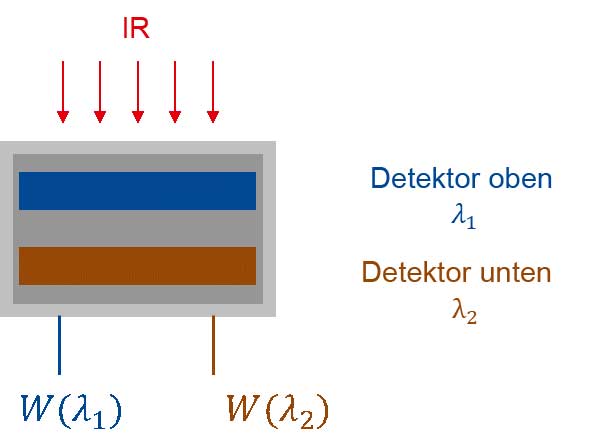
Schema eines Quotientenpyrometers mit 2 Detektoren in Sandwichbauweise
Keine Signaldämpfung
Betrachten wir im folgenden Beispiel zunächst die blaue Kurve. Das Zweifarbenthermometer ist auf einen Schwarzen Strahler (Blackbody) mit einem Emissionsgrad von 1,0 und einer Temperatur von 1500 ° C gerichtet. Basierend auf dem Planck-Gesetz liefern die beiden Detektoren bei einem Emissionsgrad von 1,0 gemäß der blauen Kurve folgende Energieeinheiten:
Detektor 1 mit Wellenlänge λ1 gibt 500 Einheiten aus
Detektor 2 mit (anderer) Wellenlänge λ2 gibt ein Signal von 1000 Einheiten aus.
Da dies ein Verhältnis-Thermometer ist, teilen wir 1000 durch 500 und erhalten ein Verhältnis von 2. Das Instrument ist so kalibriert, dass 1500 °C angezeigt werden, wenn es ein Verhältnis von 2 sieht.
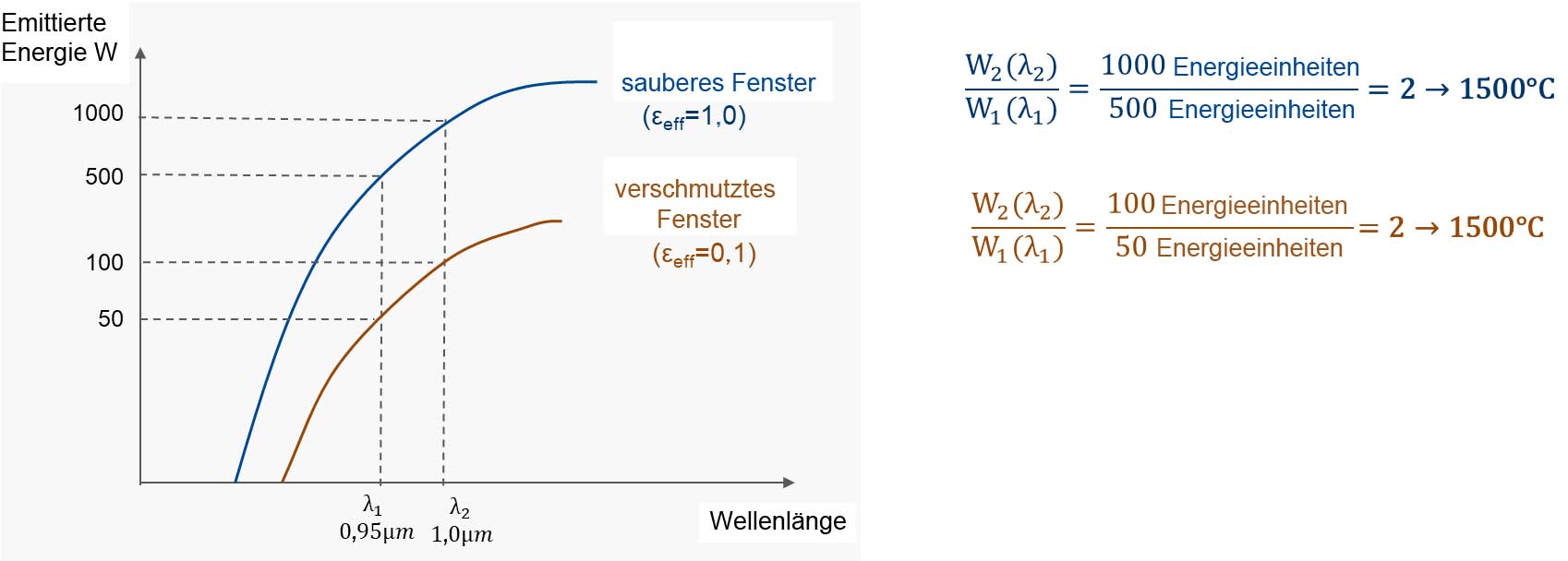
Planck-Kurven für ein Quotienten-Thermometer (zwei Messkanäle), das auf einen Schwarzen Strahler mit einer Temperatur von 1500 °C gerichtet ist
Signaldämpfung
Was passiert nun, wenn das Signal vom Messobjekts irgendwie reduziert bzw. nicht zum Detektor gelangt? Dies kann an einem verschmutzten Fenster liegen; einem Messobjekt, das zu klein ist, um den Sichtkegel auszufüllen; oder an Rauch im Gesichtsfeld des Sensors. Die braune Kurve (s. Grafik oben) zeigt ein Beispiel mit einem Signalverlust von 90 %. Die Temperatur des Messobjekts beträgt immer noch 1500 °C. Dies entspricht einem scheinbaren Emissionsgradabfall von 1,0 auf 0,1.
Detektor 1 mit Wellenlänge λ1 gibt ein Signal von 50 Einheiten aus.
Detektor 2 mit Wellenlänge λ2 gibt ein Signal von 100 Einheiten aus.
Beide Signale sind gegenüber der blauen Kurve um 90% reduziert (E = 1,0). Wie Sie sehen, ergibt 100 geteilt durch 50 wieder ein Verhältnis von 2 - das Instrument wird 1500 °C anzeigen, obwohl wir 90 % des Signals verloren haben. Jedes Zweifarbenthermometer hat eine Grenze, bis zu welcher eine Signalreduzierung zulässig ist. Dies wird als Dämpfung bezeichnet, die von 0% bis zu 95% des Signals variieren kann und dennoch eine genaue Temperatur anzeigt.
E-Slope
Grundsätzlich funktioniert ein Zweifarbenthermometer einwandfrei, solange beide Wellenlängen im gleichen Maße beeinflusst werden. Leider gibt es Anwendungen, bei denen der Emissionsgrad des Messobjekts für die beiden Wellenlängen unterschiedlich sein kann, z. B. bei der Messung von geschmolzenen Metallen. Wird das Zweifarbenthermometer auf die Metallschmelze gerichtet, ist das Signalverhältnis (oder Slope) nicht korrekt und es tritt ein Fehler bei der Temperaturmessung auf.
Wie kann das korrigiert werden? Alle Zweifarbenthermometer haben eine Einstellung namens E-Slope. Zum Betrachten der Metallschmelze muss die E-Slope-Einstellung geändert werden, bis das Instrument die korrekte Metalltemperatur anzeigt. Die korrekte Temperatur kann vorher mit einem Thermoelement ermittelt werden. Die E-Slope-Einstellung korrigiert das Verhältnis einfach um eine Konstante, welche die Instrumentenanzeige für die ungleichen spektralen Emissionsgrade des Messobjekts korrigiert. Sobald die E-Slope-Einstellung vorgenommen wurde, werden Probleme wie Rauch, Dampf, Staub, kleine Messobjekte usw. vom Instrument korrekt behandelt.
Was ist ein Pyrometer?
Ein Pyrometer ist eine Art Wärmesensor, der zum Messen von Oberflächentemperaturen verwendet wird, z.B. in Industrieöfen. Diese Geräte messen die Temperatur eines Objekts oder einer Oberfläche anhand der abgegebenen Wärmestrahlung. Dieses Verfahren wird auch als Radiometrie bezeichnet.